SIGNALS AND SYSTEMS-IV PROPERTIES OF SYSTEMS DISCRETE CONVOLUTION

EDITOR: B. SOMANATHAN NAIR

DIRECT (TABULATION) METHOD OF DISCRETE CONVOLUTION

In the direct method for performing discrete convolution, we make use of tabulation. The method is illustrated using a numerical example.

ILLUSTRATIVE EXAMPLE : Obtain the convolution of the sequences x(n) = (1, 2, 3) and h(n) = (4, 3). The bold number in these sequences represents the values of x(n) and h(n), respectively for n = 0.

Solution: For performing the desired convolution, we prepare a tabulation as shown in the convolution table using the convolution equation (1) given below.

From this basic convolution equation, we find that, for n = 0, we have

Equation (2) can be expanded as:

                y(0) = x(0)h(0) + x(1)h(-1) + x(2)h(-2) + ∙∙∙ (3)

          

The operation defined by (3) requires that we must find h(0-k) = h(- k). But we know that h(-k) is h(k) inverted or folded in time. Table 1 shows this inversion or folding operation of h(k).

Referring to Table 1, we find that its first-row entries consist of values of time factor k. Values of x(k) and h(k) are, respectively, entered in the second and third rows of Table 1.  Note that for performing convolution, we must replace n with k.  Thus, for the entries in Table 1, we have x(n) = x(k) and h(n) = h(k). Now, to get h(- k), we invert or fold h(k), with k = 0 as the fulcrum point. This operation gives the entries in the fourth row of Table 1.

After having prepared Table 1, which shows the entries x(k) and h(- k), we now turn our attention to the preparation of Table 2, which shows Table 1 added with one more row. This is to accommodate the entries from the multiplication of each of the entries of x(k) with the corresponding entries of h(- k). Looking at rows two and three, we find that the entries under the column k = - 1 are 0 and 3, which correspond to x(- 1) and  h(- 1), respectively.  The product of the two (i.e., 0 ´ 3) results in a ‘0’ [i.e., x(-1) h(-1) = 0] being entered as the product-entry under column k = - 1. Similarly, with x(0) = 1, and h(0) = 4, we  find their product  as  4. This is the entry under the column k = 0.

Now, since convolution also involves the summation of the product terms obtained in the above operation, we have to add the respective entries in the fourth row. Looking at Table 2, we find that the terms for summation are 0 (under column k = -2), 0 (under column k = -1), and 4 (under column k = 0). The sum of these three values (i.e., 0 + 4) is 4, and this is entered under the column labeled “C. Sum” (convolution sum). The fourth row is now termed y(0), as this represents the convolution sum for the situation k = 0.

            It can be seen that the terms of h(k) are not shown in Table 2, since they are no longer needed in calculations. This is to avoid the confusion, when multiplication is carried out between rows.

            Next step is to find the products and sum of the terms of x(k) and h(1- k). In this step, we find that y(0) is changed to y(1). Now, the convolution equation is

where we have shifted h(- k) by one unit to the right to get h(1 - k), as shown in Table 3.

After shifting h(-k) to the right by one unit, we multiply elements of row 2 to the corresponding elements of row 3, and add the resulting product terms. Thus, we multiply the terms 1 and 3 to get 3, and 2 and 4 to get 8. Then we add the products 3 and 8 to get the convolution sum of 11, which is then entered under the column C. Sum.

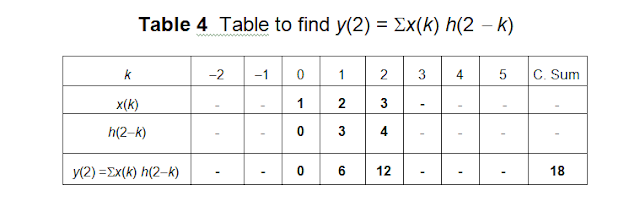
            This process of shifting h(- k) successively by one unit each,  multiplying  each of the terms of x(k) with the corresponding term of h(n - k) in each of these shifts, and adding the resulting products of each shift yield the respective convolution sums.  These actions are shown in Tables 4, 5, and 6, respectively. From Table 4, we find that the convolution sum is 18, from Table 5, we find the convolution sum is 9, and from Table 6, we find the convolution sum is 0. The computation can be seen to stop here as there are no more terms to multiply.

The convolution sum sequence can now be seen as

                                            y(n) = (4, 11, 18, 9)       (5)                                                                                                         

Figure 1 shows x(n), Fig. 2 shows h(n) and Fig. 3 shows the plot of the convolution sums.

            From (3), we find that there are four elements in the convolution sum. Notice that this was obtained as a result of convolving an input x(n) having three elements in it and impulse response h(n) having two elements in it.  It is found that the convolution length in this case

           

                                    4 = 3 + 2 - 1  (6)                                                                                               

            In general, if the length of x(n) = p bits, and that of h(n) = q bits, then we have the length L of the convolution sequence

                                                            L = p + q – 1 bits  (7)