SOLUTION OF FIRST-ORDER DIFFERENTIAL EQUATIONS –METHOD II

EDITOR: B. SOMANATHAN NAIR

1. INTRODUCTION

In electric networks, we can solve for the loop current by employing a second method as given below. This method has the advantage that we can find the steady-state solution without resorting to integration. 

Example 1: Consider the RL circuit shown in Fig. 1. At time t = 0, the switch is closed. Since the inductor opposes any sudden change in the circuit, a transient current is developed at first. After some time, the transient dies out and steady-state current flows through the circuit.

 

We can write the differential equation of the circuit as

                                   

                                                              V = iR+ Ldi/dt   (1)

           

The transient solution can be obtained from the expression

   iR+ Ldi/dt = 0  (2)

Rearranging Eq. (2), we get

                                                             di/dt = ‒iR/L (3)

Further rearrangement yields

                                                                        di/i = ‒(R/L)dt (4)

Integrating Eq. (4) gives

                                                            ln I = ‒ (R/L)t+ ln A  (5)

where ln A is the constant of integration. From Eq. (5), we get

                                                            ln (i/A) = ‒ (R/L)t  (6)

Taking antilog of Eq. (6), we obtain the transient solution

  i_tr = Ae^‒(R/L)t     (7)

Now, after the transient has died out, a constant (steady-state) current flows through the circuit. This current can be obtained, since inductance L = 0 under steady-state condition, as

                                                            i_ss = V/R   (8)

Combining the steady-state and transient currents, we find

                                                i_total  = i_tr + i_ss =  Ae^‒(R/L)t + V/R  (9)

To evaluate A, we find that at t = 0, L acts as an open circuit, and hence i(0) = 0. Using this condition, we have from Eq. (9) 

                                                            0 =  A+ V/R  (10)

From which, we obtain

                                                            A = ‒V/R   (11)

The complete solution therefore becomes

                                                   i_total  = (V/R)[1‒ e^‒(R(L)t] (12)

The technique mentioned above becomes advantageous in solving problems with alternating currents, where the integration is slightly difficult.  

2. SOLUTION OF EXAMPLE 1 USING THE GENERAL EQUATION

Solution of first-order differential equation (dy/dt)+ py = q is

                                             y = A e^‒pt+ e^‒pt ∫qe^ptdt (13)

The differential equation of the given problem is

                                                            L(di/dt) +Ri = V (14)

Rearranging Eq. (14), we obtain

                                                     (di/dt) +(R/L) i = V/L (15)

In Eq. (15), we find p = R/L, and q = V/L. Using these in Eq. (13), we get

                                                i = A e^‒(R/L)t+ e^‒(R/L)t ∫(V/L) e^‒(R/L)t dt (16)

Carrying out the integration in the second term of RHS yields

                                                  i = A e^‒(R/L)t+V/R  (17)

Equation (17) is the same as Eq. (9) in the first solution. The rest of the solution is therefore the same as in Solution I.

3. AC TRANSIENT USING METHOD II 

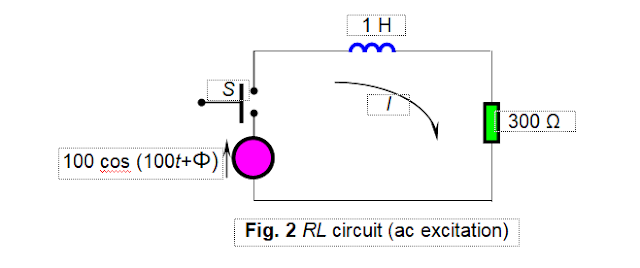
Example 2: Find the current in the circuit shown in Fig. 2. The circuit is excited by the ac voltage, given by the expression 100 cos (100t + Φ). The  Switch is closed when Φ = 45^o.

 

Solution: The differential equation governing the circuit is

                                                 di/dt + 300i = 100 cos (100t+Φ)

The transient solution obtained from the equation

                                                         di/dt + 300i = 0

Separating the variables and integrating the resultant function yields

                                                         i_tr  = Ae^‒300t

To find the steady-state condition, we use the second method. In this, we find that under steady-state condition, the current in an RL circuit is given by

                        i_ss = V/√(R² + X²) = (100)/√(R² + ω²L²) ∟‒ tan^-1(100/300)

                                                                                                                                                                                                                                                                                                                                                        = 100/√(300²+100²) ∟‒tan^-1(1/3)

                                                           

                                                     =  100/316.28 = 0.316 ∟‒18.43^o

The complete solution, therefore, is

                        i = i_tr + i_ss = Ae^‒300t + 0.316 cos (100t + Φ ‒ 18.43^o)    (1)

Now, to evaluate A, we use the boundary condition: at t = 0, L is open and hence current i = 0. Using this, with Φ = 45, we obtain from Eq. (1)

                                            0  = A + 0.316 cos (45 ^o ‒18.43^o) = A + 0.282

Then 

                                                              A  =  ‒ 0.282

The compete solution, hence becomes (with 45 ^o ‒18.43^o = 26.57^o)

                                                i = ‒ 0.282e^‒300t + 0.316 cos (100t+26.57^o)

It can be seen that the computation is comparatively simple in this method.